基于 GD32F303ZET6 苹果派开发板
简介
上一章中,我们介绍了如何制作仪表盘。当时的仪表盘指针是通过画线实现的,简陋,不好看,本章中我们将介绍如何通过多边形填充的方式绘制指针。
菱形指针
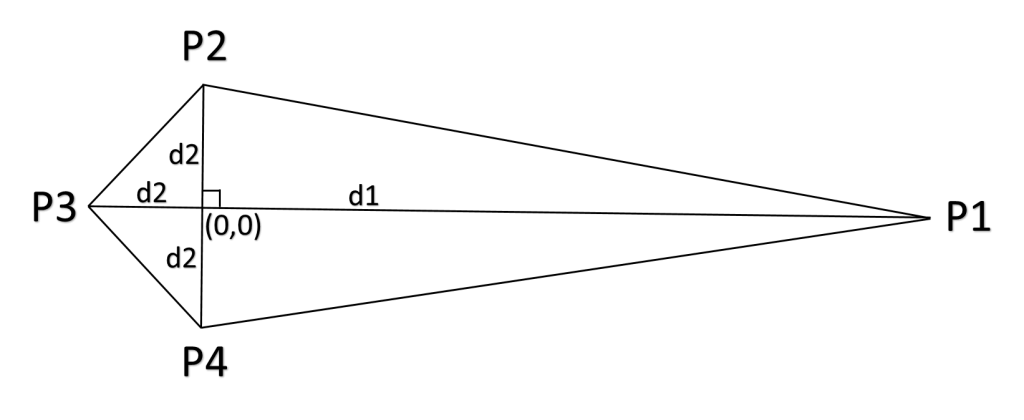
仪表盘中,最简单的莫过于菱形指针。菱形指针具体如下所示。使用多边形填充的方式绘制菱形指针时,我们需要提供四个顶点的具体坐标。在本文中,菱形指针默认方向朝右,以中心交点处为原点。d1 和 d2 的长度确定好后,以水平向右为 0°,根据指针的旋转角度,P1~P4 的坐标就可以通过几何关系求解出来。
如何判断点是否在多边形内
EasyX 同样也提供了多边形填充的 API 接口,可是为了方便移植到单片机平台,我们还是要实现一下自己的多边形填充函数。多边形填充的难点在于如何判断出某一个坐标点是否落在多边形区域内。多边形填充时,一般是求解出一个刚好可以容纳这个多边形的矩形区域,这个不难做到;然后,从头到尾扫描这个矩形区域,如果坐标点落到了多边形区域内,就绘制该坐标点,否则便跳过。
那么如何判断坐标点是否落在多边形区域内呢?这个网上有不少的文章解释,在此不过多分析,只需要知道怎么用即可(其实我也不懂,这代码是网上抄的)。C 语言实现的代码如下所示。
#define MAX_POLY_NUM 16 //最多的顶点数量
//了提升速度在这个例子中使用的全局变量。 可以按需要改变
static int s_iPolyCorners; //顶点数量
static float s_arrPolyX[MAX_POLY_NUM]; //顶点横坐标
static float s_arrPolyY[MAX_POLY_NUM]; //顶点纵坐标
/*********************************************************************************************************
* 函数名称: IsInPolygon
* 函数功能: 判断坐标点是否在多边形中
* 输入参数: x、y:坐标值
* 输出参数: void
* 返 回 值: 0-该点不在多边形区域内,其它-该点处于多边形中
* 创建日期: 2023年03月14日
* 注 意: 如果点 x,y 在多边形内则该函数会返回非零值,否则返回零值
* 如果点正好在多边形的边上,那么这个函数会返回非零值或者零值
*********************************************************************************************************/
static char IsInPolygon(int x, int y)
{
int i, j = s_iPolyCorners - 1;
char oddNodes = 0;
for (i = 0; i < s_iPolyCorners; i++) {
if ((s_arrPolyY[i] < y && s_arrPolyY[j] >= y
|| s_arrPolyY[j] < y && s_arrPolyY[i] >= y)
&& (s_arrPolyX[i] <= x || s_arrPolyX[j] <= x)) {
oddNodes ^= (s_arrPolyX[i] + (y - s_arrPolyY[i]) / (s_arrPolyY[j] - s_arrPolyY[i]) * (s_arrPolyX[j] - s_arrPolyX[i]) < x);
}
j = i;
}
return oddNodes;
}多边形填充
知道了如何判断坐标点是否在多边形区域后,多边形填充就变得简单了起来,具体如下所示。需要注意的是,IsInPolygon 函数判断边沿点可能会有误差,所以要用划线的方式绘制边沿,如此一来就可以实现一个完美的多边形填充了。
/*********************************************************************************************************
* 函数名称: PolygonFill
* 函数功能: 多边形填充
* 输入参数: num :顶点数量
* px :顶点横坐标值
* py :顶点纵坐标值
* color:填充颜色
* 输出参数: void
* 返 回 值: void
* 创建日期: 2023年03月14日
* 注 意:
*********************************************************************************************************/
void PolygonFill(unsigned int num, unsigned int* px, unsigned int* py, unsigned int color)
{
int i;
int x0, y0, x1, y1, x, y;
//顶点数量过多或过少
if ((num > MAX_POLY_NUM) || (num < 3))
{
while (1) {}
}
//备份顶点数量
s_iPolyCorners = num;
//备份坐标点
for (i = 0; i < num; i++)
{
s_arrPolyX[i] = px[i];
s_arrPolyY[i] = py[i];
}
//确定显示区域
x0 = px[0]; y0 = py[0]; x1 = px[0]; y1 = py[0];
for (i = 0; i < num; i++)
{
if (px[i] < x0)
{
x0 = px[i];
}
if (px[i] > x1)
{
x1 = px[i];
}
if (py[i] < y0)
{
y0 = py[i];
}
if (py[i] > y1)
{
y1 = py[i];
}
}
//画边框
for (i = 0; i < num - 1; i++)
{
LCDDrawLine(px[i], py[i], px[i + 1], py[i + 1], color);
}
LCDDrawLine(px[0], py[0], px[num - 1], py[num - 1], color);
//遍历所有点
for (y = y0; y <= y1; y++)
{
for (x = x0; x <= x1; x++)
{
if (0 != IsInPolygon(x, y))
{
LCDFastDrawPoint(x, y, color);
}
}
}
}
绘制仪表盘指针
有了多边形填充组件后,绘制仪表盘指针就变得非常简单,只需要根据几何关系,将各个顶点的坐标求解出来,带入多边形填充函数即可,具体如下所示。需要注意的是,Y 方向与屏幕的 Y 方向反了,所以计算偏移量的时候要取个反。
绘制指针的时候,可以根据需要将指针分割成几个部分,填充不同的颜色,可以有效提高指针的立体感。例如指针下半部分的颜色较深一些,就可以做出立体感。
//指针相关信息
#define POINTER_X0 (400)
#define POINTER_Y0 (260)
#define POINTER_COLOR (LCD_COLOR_RED)
#define POINTER_D1 (200)
#define POINTER_D2 (5)
//设置仪表盘显示
//speed:0-1200
void SetSpeedometer(unsigned int speed)
{
static unsigned int s_arrPointerX[4] = { 0 };
static unsigned int s_arrPointerY[4] = { 0 };
double pi, angle0, angle1, angle, rate;
int x, y, x0, y0, x1, y1;
//限定范围
if (speed > 1200)
{
speed = 1200;
}
//锁定 LCD
LCDLock();
//绘制背景
DrawBackground();
//计算占比大小
rate = 100.0 * (double)speed / 1200.0;
rate = 100.0 - rate;
//求直线在直角坐标系中的角度
pi = 3.1415926535;
angle0 = pi * -0.2445; //100%对应的角度(弧度)
angle1 = pi * 1.2445; //0%对应的角度(弧度)
angle = angle0 + (angle1 - angle0) * rate / 100.0;
//求 P1 点坐标
x = POINTER_D1 * cos(angle);
y = POINTER_D1 * sin(angle);
y = -y;
s_arrPointerX[0] = POINTER_X0 + x;
s_arrPointerY[0] = POINTER_Y0 + y;
//求 P2 点坐标
angle = angle + 0.5 * pi;
x = POINTER_D2 * cos(angle);
y = POINTER_D2 * sin(angle);
y = -y;
s_arrPointerX[1] = POINTER_X0 + x;
s_arrPointerY[1] = POINTER_Y0 + y;
//求 P3 点坐标
angle = angle + 0.5 * pi;
x = POINTER_D2 * cos(angle);
y = POINTER_D2 * sin(angle);
y = -y;
s_arrPointerX[2] = POINTER_X0 + x;
s_arrPointerY[2] = POINTER_Y0 + y;
//求 P4 点坐标
angle = angle + 0.5 * pi;
x = POINTER_D2 * cos(angle);
y = POINTER_D2 * sin(angle);
y = -y;
s_arrPointerX[3] = POINTER_X0 + x;
s_arrPointerY[3] = POINTER_Y0 + y;
//多边形填充
PolygonFill(4, s_arrPointerX, s_arrPointerY, POINTER_COLOR);
//解锁 LCD
LCDUnlock();
}实验结果
最后的实验结果如下所示。指针可能会比较闪,是因为刷新的区域很大。读者可以参考上一篇文章,将指针的刷新区域设置的小一些,这样就很平稳了。
-多边形填充-实验结果-20230314.bmp)
源码
本章节中的源码请参考《单片机 GUI 设计(零)- 大纲》
