算法笔记
包含的头文件
代码如下:
#include "math.h"
#include "malloc.h"均匀分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Uniform
* 函数功能: 生成均匀分布的随机数
* 输入参数: a:区间下限
* b:区间上限
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Uniform(double a, double b, long int* seed)
{
double t;
*seed = 2045 * (*seed) + 1;
*seed = *seed - (*seed / 1048576) * 1048576;
t = (*seed) / 1048576.0;
t = a + (b - a) * t;
return t;
}在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。第一条曲线为概率密度函数所对应的曲线。第二条曲线表示在 -50~50 这个区间内,取 1000 等份,统计落到这个区间内的测量值的数量。从第二条曲线可以看出,落到每个区间内的测量值的数量很均匀,大致在 9960~10040 这个范围之内,平均值为 10000。平均值是 10000,乘上区间数量 1000,正好是等于测量次数一千万。
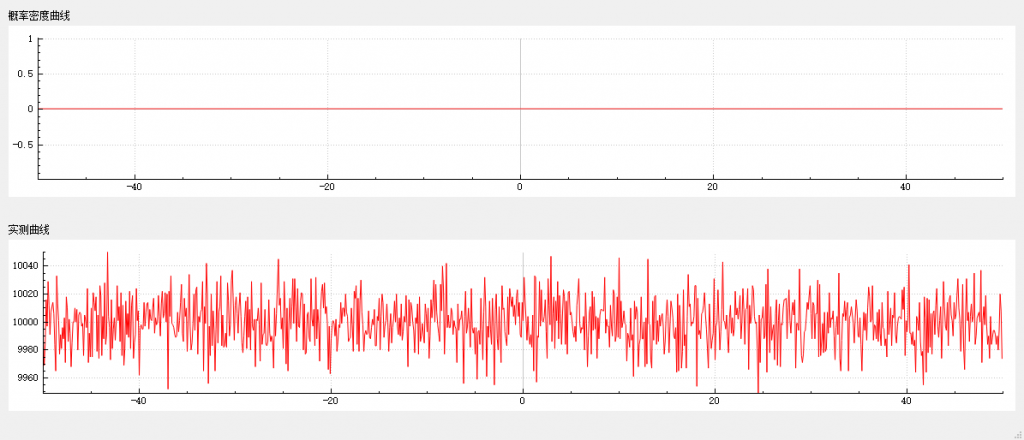
正态分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Gauss
* 函数功能: 生成正态分布的随机数
* 输入参数: mean:正态分布的均值μ
* sigma:正态分布的均方差σ
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Gauss(double mean, double sigma, long int* seed)
{
int i;
double x, y;
for (x = 0, i = 0; i < 12; i++)
{
x += Uniform(0.0, 1.0, seed);
}
x = x - 6.0;
y = mean + x * sigma;
return y;
}
在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
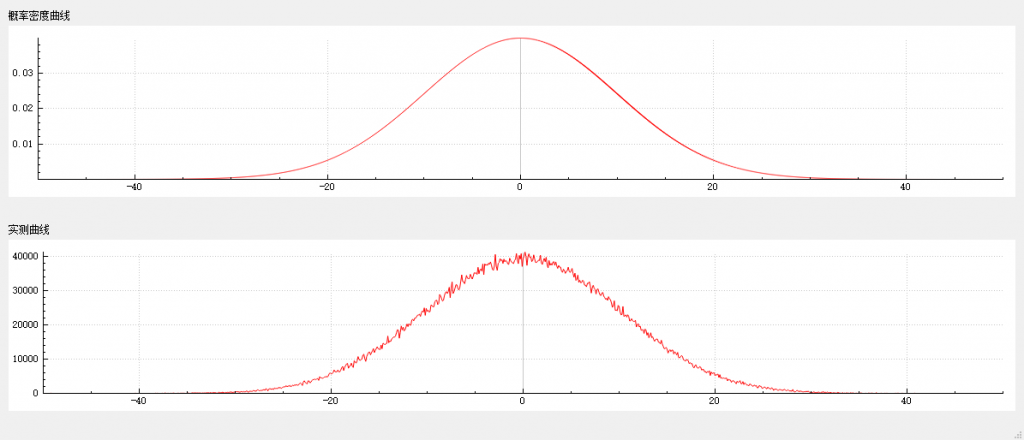
指数分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Exponent
* 函数功能: 生成指数分布的随机数
* 输入参数: beta:指数分布的均值β
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Exponent(double beta, long int* seed)
{
double u, x;
u = Uniform(0.0, 1.0, seed);
x = -beta * log(u);
return x;
}在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
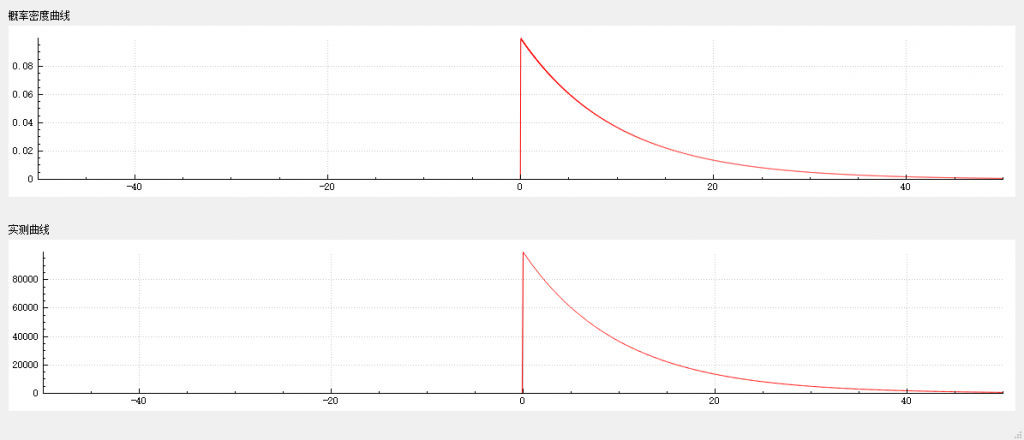
拉普拉斯分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Laplace
* 函数功能: 生成拉普拉斯分布的随机数
* 输入参数: beta:拉普拉斯分布的参数β
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Laplace(double beta, long int* seed)
{
double u1, u2, x;
u1 = Uniform(0.0, 1.0, seed);
u2 = Uniform(0.0, 1.0, seed);
if (u1 <= 0.5)
{
x = -beta * log(1.0 - u2);
}
else
{
x = beta * log(u2);
}
return x;
}在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
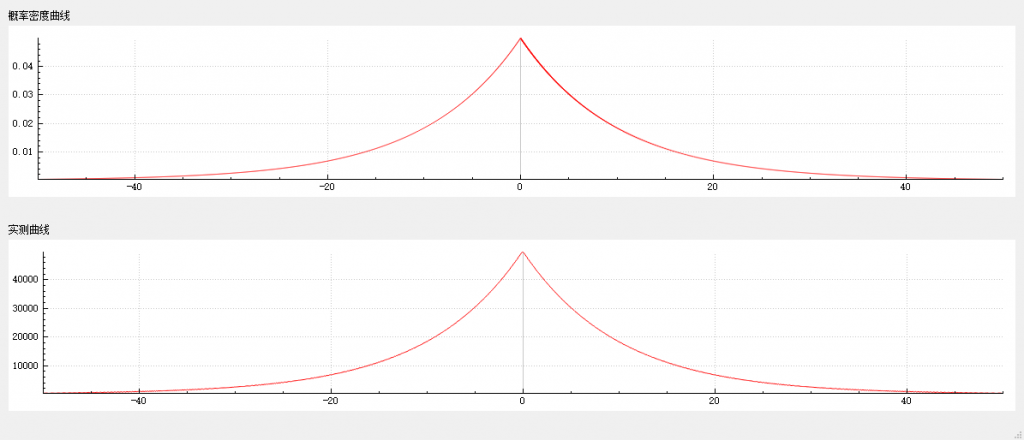
瑞利分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Rayleigh
* 函数功能: 生成瑞利分布的随机数
* 输入参数: beta:瑞利分布的参数β
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Rayleigh(double sigma, long int* seed)
{
double u, x;
u = Uniform(0.0, 1.0, seed);
x = -2.0 * log(u);
x = sigma * sqrt(x);
return x;
}在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
对数正态分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Lognorm
* 函数功能: 生成对数正态分布的随机数
* 输入参数: mean:对数正态分布的参数μ
* sigma:对数正态分布的参数σ
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Lognorm(double mean, double sigma, long int* seed)
{
double x, y;
y = Gauss(mean, sigma, seed);
x = exp(y);
return x;
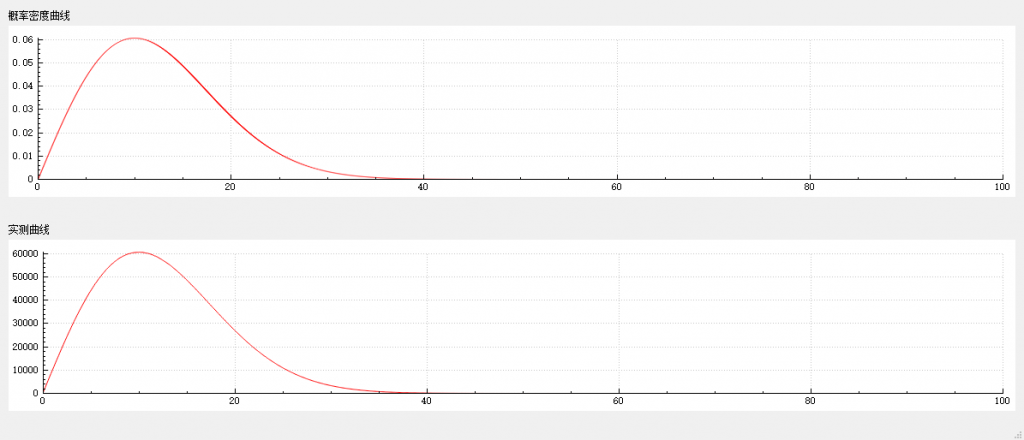
}在 0~10 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
柯西分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Cauchy
* 函数功能: 生成柯西分布的随机数
* 输入参数: alpha:柯西分布的参数α
* beta:柯西分布的参数β
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Cauchy(double alpha, double beta, long int* seed)
{
double u, x;
u = Uniform(0.0, 1.0, seed);
x = alpha - beta / tan(3.1415926 * u);
return x;
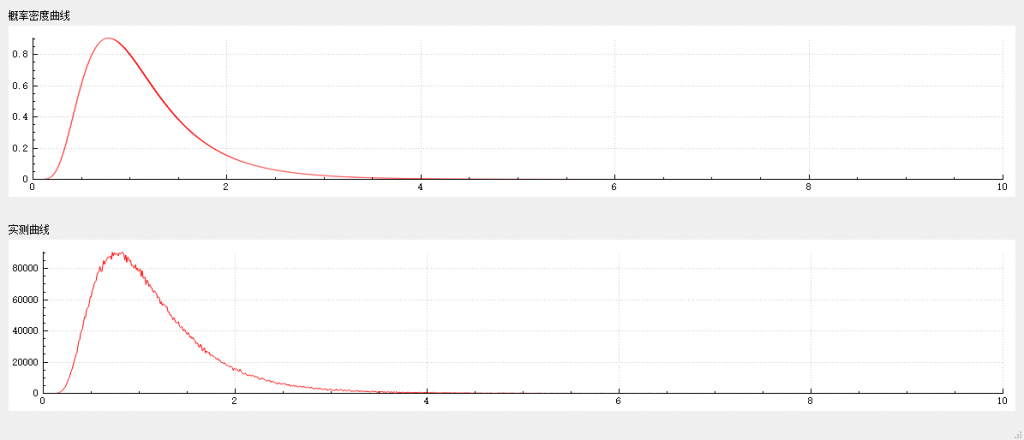
}在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
韦伯分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Weibull
* 函数功能: 生成韦伯分布的随机数
* 输入参数: alpha:韦伯分布的参数α
* beta:韦伯分布的参数β
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Weibull(double alpha, double beta, long int* seed)
{
double u, x;
u = Uniform(0.0, 1.0, seed);
u = -log(u);
x = beta * pow(u, 1.0 / alpha);
return x;
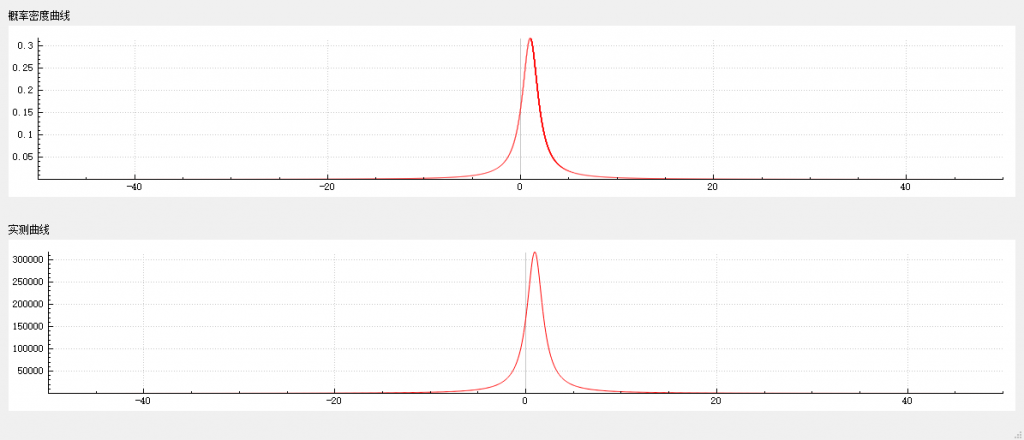
}在 0~5 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
埃尔朗分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Erlang
* 函数功能: 生成埃尔朗分布的随机数
* 输入参数: m:埃尔朗分布的参数m
* beta:埃尔朗分布的参数β
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Erlang(double m, double beta, long int* seed)
{
int i;
double u, x;
for (u = 1.0, i = 0; i < m; i++)
{
u *= Uniform(0.0, 1.0, seed);
}
x = -beta * log(u);
return x;
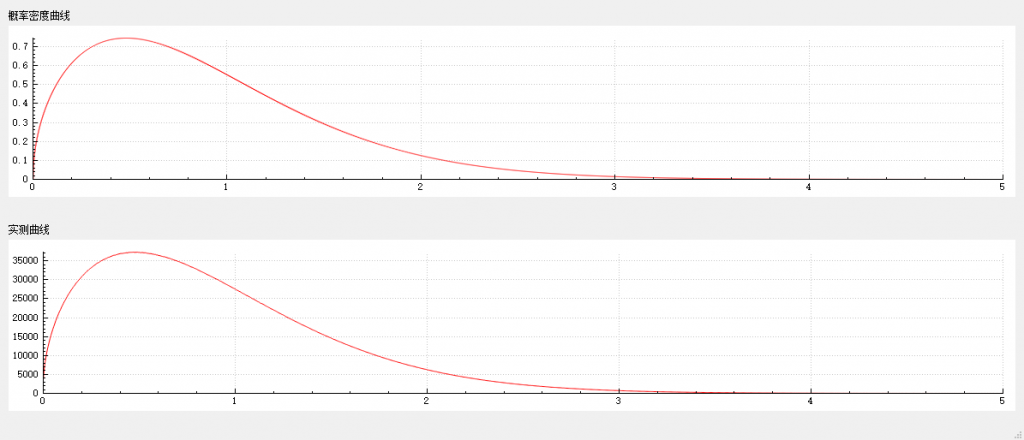
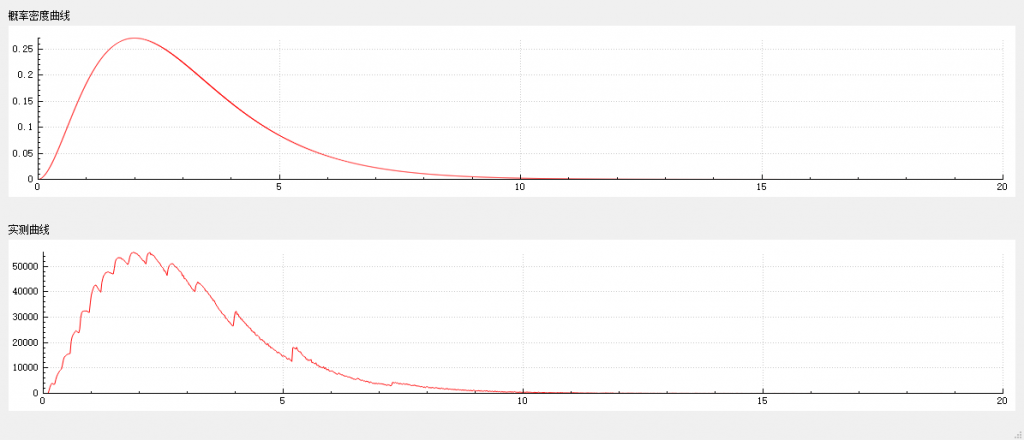
}在 0~20 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
贝努里分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Bn
* 函数功能: 生成贝努里分布的随机数
* 输入参数: m:贝努里分布的参数p
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
int Bn(double p, long int* seed)
{
int x;
double u;
u = Uniform(0.0, 1.0, seed);
x = (u <= p) ? 1:0;
return x;
}贝努里-高斯分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Bg
* 函数功能: 生成贝努里-高斯分布的随机数
* 输入参数: m:贝努里分布的参数p
* mean:高斯分布的均值μ
* sigma:高斯分布的均方差σ
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
double Bg(double p, double mean, double sigma, long int* seed)
{
double u, x;
u = Uniform(0.0, 1.0, seed);
if (u <= p)
{
x = Gauss(mean, sigma, seed);
}
else
{
x = 0.0;
}
return x;
}
二项式分布的随机数
代码如下
/*********************************************************************************************************
* 函数名称: Bin
* 函数功能: 生成二项式分布的随机数
* 输入参数: n:二项式分布的参数n
* p:二项式分布的参数μ
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
int Bin(int n, double p, long int* seed)
{
int i;
double x;
for (x = 0.0, i = 0; i < n; i++)
{
x += Bn(p, seed);
}
return x;
}泊松分布的随机数
代码如下:
/*********************************************************************************************************
* 函数名称: Poisson
* 函数功能: 生成泊松分布的随机数
* 输入参数: n:泊松分布的均值λ
* seed:随机数种子
* 输出参数: void
* 返 回 值: 随机数
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
int Poisson(double lambda, long int* seed)
{
int i, x;
double a, b, u;
a = exp(-lambda);
i = 0;
b = 1.0;
do
{
u = Uniform(0.0, 1.0, seed);
b *= u;
i++;
}while(b >= a);
x = i - 1;
return x;
}在 -50~50 区间内,随机数种子为 13579 的条件下,连续获取一千万个随机数,测量结果如下。
ARMA(p,q) 模型数据
代码如下:
/*********************************************************************************************************
* 函数名称: ARMA
* 函数功能: 生成 ARMA(p,q) 模型数据
* 输入参数: a:双精度实型一维数组,长度为(p+1)。ARMA(p,q) 模型的自回归系数。
* b:双精度实型一维数组,长度为(p+1)。ARMA(p,q) 模型的滑动平均系数。
* p:整形变量。ARMA(p,q) 模型的自回归阶数。
* q:整形变量。ARMA(p,q) 模型的滑动平均阶数。
* mean:双精度实型变量。产生白噪声所用的正态分布的均值μ。
* sigma:双精度实型变量。产生白噪声所用的正态分布的均方差σ
* seed:长整型指针变量。*seed 为随机数种子。
* x:双精度实型一维数组,长度为 n。存放 ARMA(p,q) 模型的数据。
* n:整型变量。ARMA(p,q) 模型数据的长度。
* 输出参数: void
* 返 回 值: void
* 创建日期: 2023年08月10日
* 注 意:
*********************************************************************************************************/
void ARMA(double* a, double* b, int p, int q, double mean, double sigma, long int* seed, double* x, int n)
{
int i, k, m;
double s;
double* w;
w = malloc(n * sizeof(double));
for (k = 0; k < n; k++)
{
w[k] = Gauss(mean, sigma, seed);
}
x[0] = b[0] * w[0];
for (k = 1; k <= p; k++)
{
s = 0.0;
for (i = 1; i <= k; i++)
{
s += a[i] * x[k - i];
}
s = b[0] * w[k] - s;
if (q == 0)
{
x[k] = s;
continue;
}
m = (k > q)? q:k;
for (i = 1; i <= m; i++)
{
s += b[i]*w[k - i];
}
x[k] = s;
}
for (k = (p + 1); k <= n; k++)
{
s = 0.0;
for (i = 1; i <= p; i++)
{
s += a[i] * x[k - i];
}
s = b[0] * w[k] - s;
if (q == 0)
{
x[k] = s;
continue;
}
for (i = 1; i <= q; i++)
{
s += b[i] * w[k - i];
}
x[k] = s;
}
free(w);
}含有高斯白噪声的正弦组合信号
代码如下:
/*********************************************************************************************************
* 函数名称: Sinwn
* 函数功能: 生成含有高斯白噪声的正弦组合信号
* 输入参数: a:双精度实型一维数组,长度为 m。各正弦信号的振幅。
* f:双精度实型一维数组,长度为 m。各正弦信号的频率。
* ph:双精度实型一维数组,长度为 m。各正弦信号的相位。
* m:整型变量。正弦信号的个数。
* fs:双精度实型变量。采样频率,单位是 Hz。
* snr:双精度实型变量。信噪比,单位是 dB。
* seed:长整型变量。随机数的种子。
* x:双精度实型一维数组,长度为 n。存放所产生的数据
* n:整型变量。数据长度
* 输出参数: void
* 返 回 值: void
* 创建日期: 2023年08月11日
* 注 意:
*********************************************************************************************************/
void Sinwn(double* a, double* f, double* ph, int m, double fs, double snr, long int* seed, double* x, int n)
{
int i, k;
double z, pi, nsr;
pi = 4.0 * atan(1.0);
z = snr / 10.0;
z = pow(10.0, z);
z = 1.0 / (2.0 * z);
nsr = sqrt(z);
for (i = 0; i < m; i++)
{
f[i] = 2.0 * pi * f[i] / fs;
ph[i] = ph[i] * pi / 180.0;
}
for (k = 0; k < n; k++)
{
x[k] = 0.0;
for (i = 0; i < m; i++)
{
x[k] = x[k] + a[i] * sin(k * f[i] + ph[i]);
}
x[k] = x[k] + nsr * Gauss(0.0, 1.0, seed);
}
}